3 1 2 Times 3
Lesson 4: Multiplying and Dividing Fractions
/en/fractions/adding-and-subtracting-fractions/content/
Multiplying fractions
A fraction is a part of a whole. In the last lesson, you learned how to add together and subtract fractions. But that'south not the only kind of math yous can do with fractions. There are times when it will be useful to multiply fractions too.
Click through the slideshow to learn how to write a multiplication trouble with fractions.
Attempt This!
Effort setting upward the multiplication problem below. Don't worry nearly solving it yet!
A recipe calls for 2/3 of a cup of milk. You want to cut the recipe in half.

Annotation: Although our case says the correct answer is 2/3 x one/ii, remember, with multiplying order does not matter. i/2 x two/iii would too be correct.
Solving multiplication bug with fractions
Now that we know how to set upward multiplication bug with fractions, let'south practice solving a few. If you experience comfortable multiplying whole numbers, you're ready to multiply fractions.
Click through slideshow to learn how to multiply two fractions.
Try This!
Try solving the multiplication problems below.
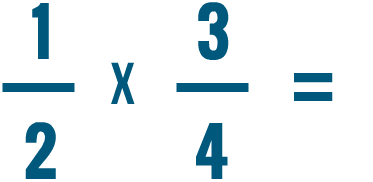
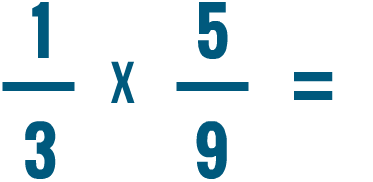
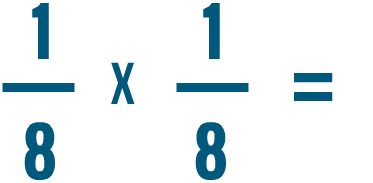
Multiplying a fraction and a whole number
Multiplying a fraction and a whole number is similar to multiplying 2 fractions. In that location'due south simply one extra footstep: Before you can multiply, y'all'll need to turn the whole number into a fraction. This slideshow will show yous how to practice it.
Click through the slideshow to larn how to multiply a fraction and a whole number.
Try This!
Try solving the multiplication problems below.
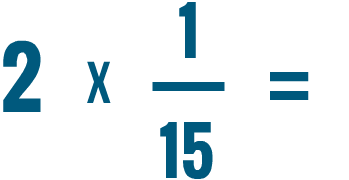
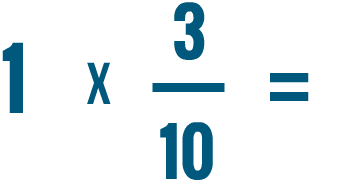
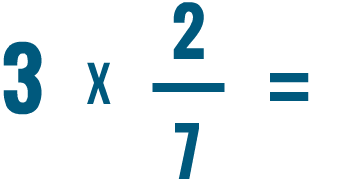
Dividing fractions
Over the last few pages, you've learned how to multiply fractions. Y'all might accept guessed that you lot tin divide fractions also. Yous split fractions to come across how many parts of something are in something else. For instance, if you wanted to know how many fourths of an inch are in four inches, you could split up 4 by 1/iv.
Allow's try another case. Imagine a recipe calls for 3 cups of flour, but your measuring loving cup simply holds 1/3, or ane-third, of a loving cup. How many thirds of a cup should you add?
We'll need to find out how many thirds of a loving cup are in three cups. In other words, we'll demand to separate three by one-tertiary.
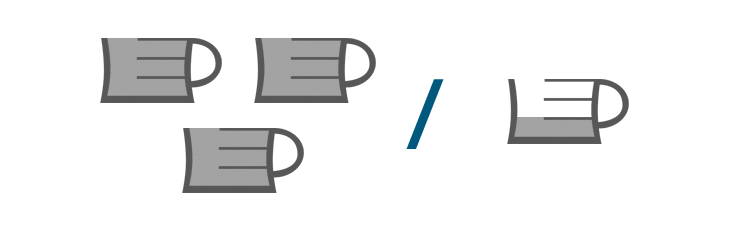
We'd write the problem like this:
3 ÷ 1/iii
Try This!
Try setting up these partition problems with fractions. Don't worry almost solving them yet!
A recipe calls for 3/4 of a cup of water. You only take a i/8 measuring cup.

Solving division issues with fractions
Now that nosotros know how to write sectionalisation problems, let's practice by solving a few. Dividing fractions is a lot like multiplying. Information technology merely requires one actress step. If you tin multiply fractions, you can divide them too!
Click through the slideshow to acquire how to divide a whole number by a fraction.
Try This!
Endeavor solving these partition problems. Don't worry about reducing the reply for at present.
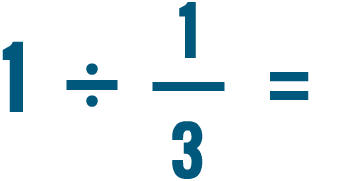
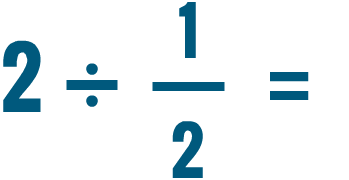
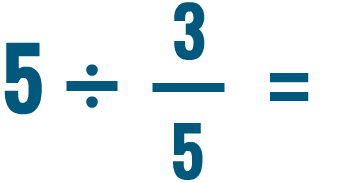
Dividing two fractions
We just learned how to divide a whole number by a fraction. Yous can use the same method to separate two fractions.
Click through the slideshow to acquire how to dissever with ii fractions.
Try This!
Effort solving these segmentation problems. Don't worry about reducing the answer for at present.
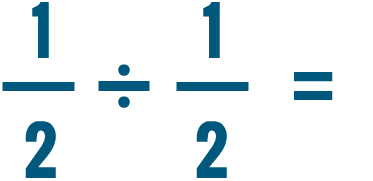
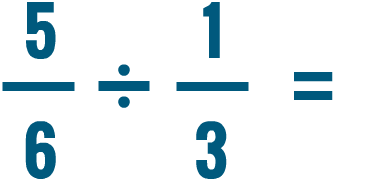
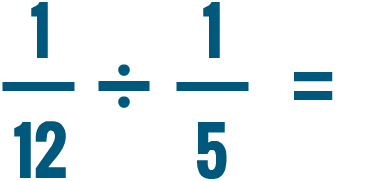
Multiplying and dividing mixed numbers
How would you solve a problem like this?
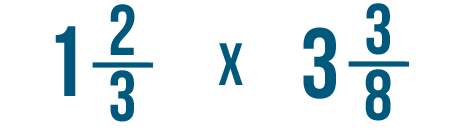
As you learned in the previous lesson, whenever you're solving a problem with a mixed number you'll need to convert it into an improper fraction first. So you can multiply or divide as usual.
Using canceling to simplify problems
Sometimes you might take to solve issues like this:
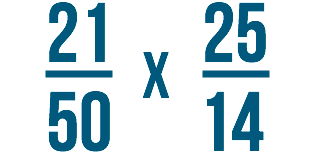
Both of these fractions include large numbers. You could multiply these fractions the same fashion as whatever other fractions. However, large numbers like this can be hard to understand. Can you film 21/50, or twenty-one fiftieths, in your head?
21/50 x 25/14 = 525/700
Even the reply looks complicated. It's 525/700, or 5 hundred twenty-5 seven-hundredths. What a mouthful!
If you don't like working with large numbers, you can simplify a problem like this by using a method called canceling. When y'all cancel the fractions in a problem, y'all're reducing them both at the same time.
Canceling may seem complicated at outset, simply we'll show you how to practice information technology step past step. Let'southward take another look at the example we just saw.
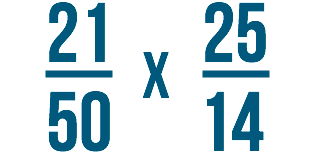
Step 1
Starting time, look at the numerator of the start fraction and the denominator of the 2nd. Nosotros want to see if they can be divided past the same number.
In our example, it looks like both 21 and fourteen can be divided by seven.
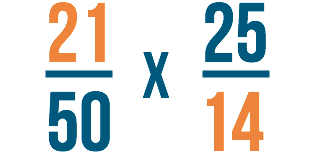
Step 2
Side by side, we'll carve up 21 and 14 by 7. Beginning, we'll divide our height number on the left: 21.
21 ÷ 7 = 3
So we'll divide the bottom number on the correct: fourteen.
14 ÷ 7 = two
We'll write the answers to each problem adjacent to the numbers nosotros divided. Since 21 ÷ vii equals 3, we'll write three where the 21 was. 14 ÷ vii equals ii, so nosotros'll write 2 where the 14 was. We can cross out, or cancel, the numbers nosotros started with.
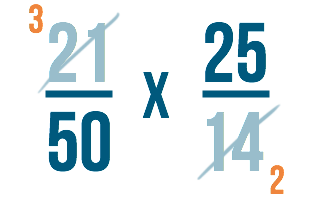
Our trouble looks a lot simpler now, doesn't information technology?
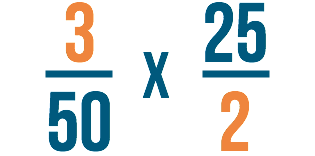
Step 3
Permit's look at the other numbers in the fraction. This time we'll expect at the denominator of the offset fraction and the numerator of the 2nd. Can they be divided by the same number?
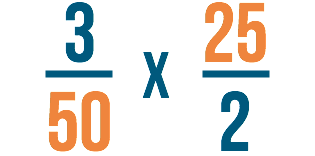
Find they tin can both exist divided by 25! You might have as well noticed they can both exist divided past 5. We could use 5 too, but generally when you are canceling, you want to wait for the biggest number both numbers tin be divided by. This style you won't have to reduce the fraction again at the end.
Footstep iv
Adjacent, we'll cancel merely similar we did in step 2.
We'll separate our bottom number on the left: 50.
50 ÷ 25 = 2
Then we'll carve up the top number on the right: 25.
25 ÷ 25 = i
We'll write the answers to each problem next to the numbers we divided.
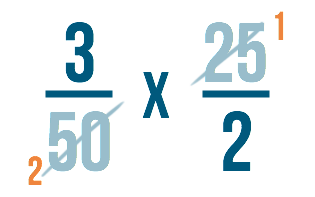
Step 5
At present that we've canceled the original fractions, we tin can multiply our new fractions like we normally would. Every bit e'er, multiply the numerators first:
three x 1 = iii
And so multiply the denominators:
2 x 2 = 4
So three/2 x 1/ii = 3/four, or three-fourths.
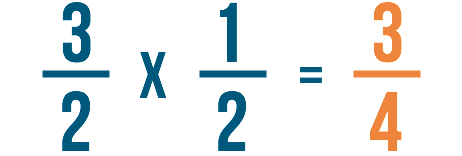
Step 6
Finally, let'southward double cheque our work. 525/700 would have been our respond if we had solved the problem without canceling. If we divide both 525 and 700 by 175, we can see that 525/700 is equal to three/4.
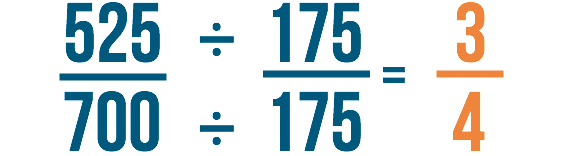
We could likewise say that nosotros're reducing 525/700 to 3/4. Remember, canceling is just another manner of reducing fractions before solving a trouble. You'll get the same respond, no matter when you reduce them.
/en/fractions/converting-percentages-decimals-and-fractions/content/
3 1 2 Times 3,
Source: https://edu.gcfglobal.org/en/fractions/multiplying-and-dividing-fractions/1/
Posted by: baltzcoonly63.blogspot.com



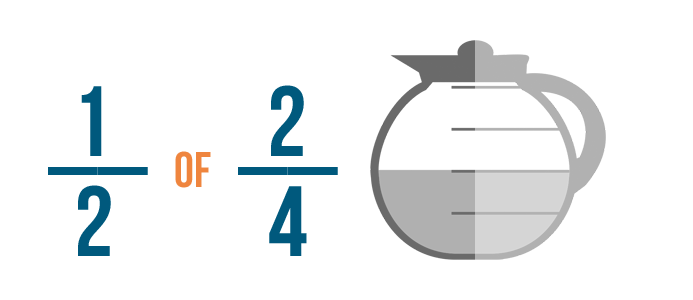
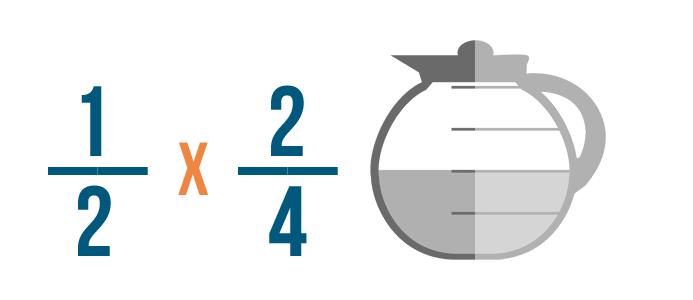
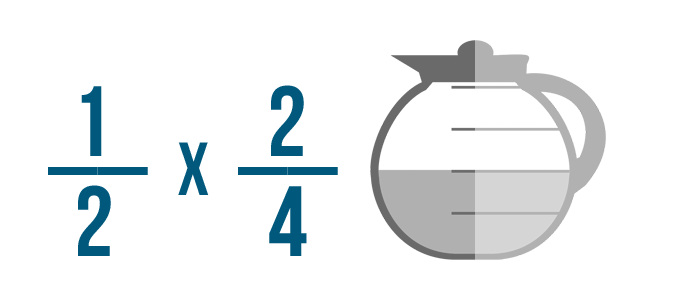
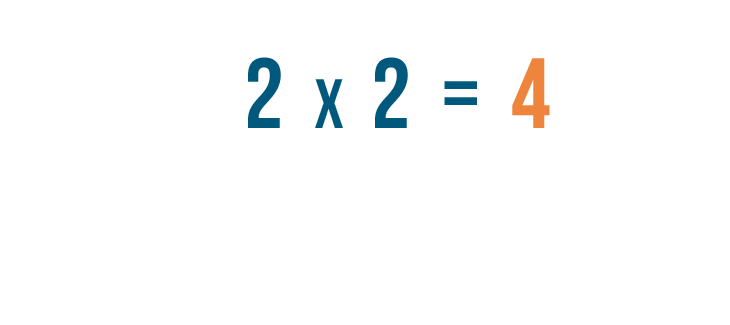
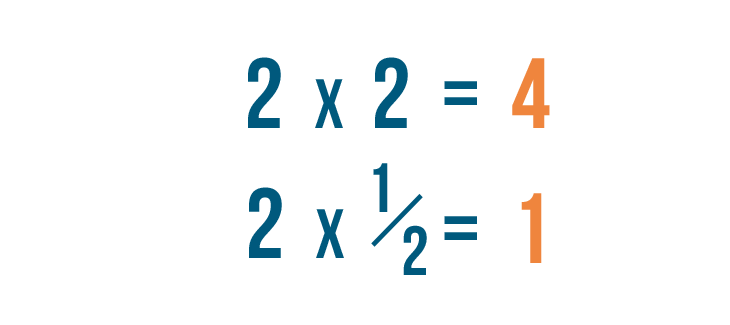

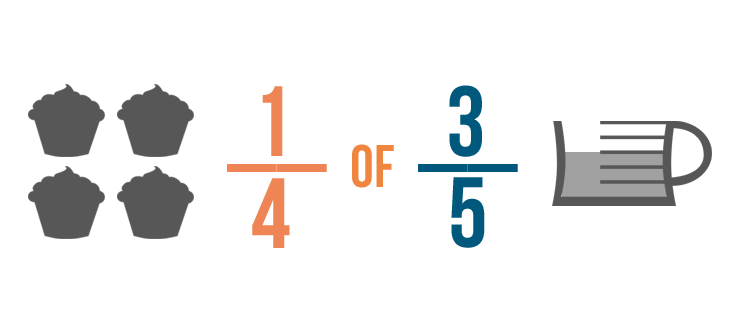
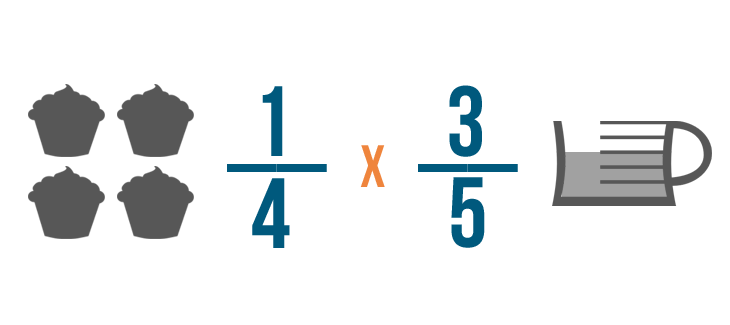
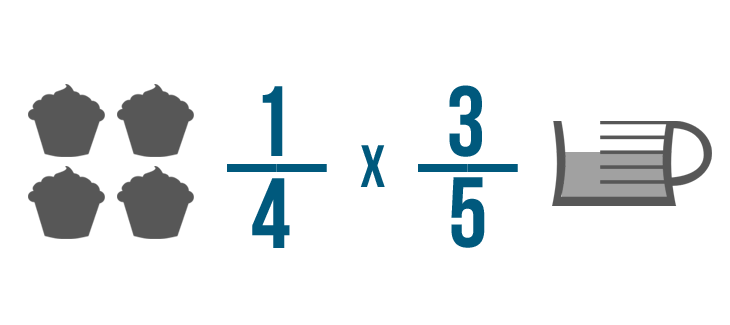

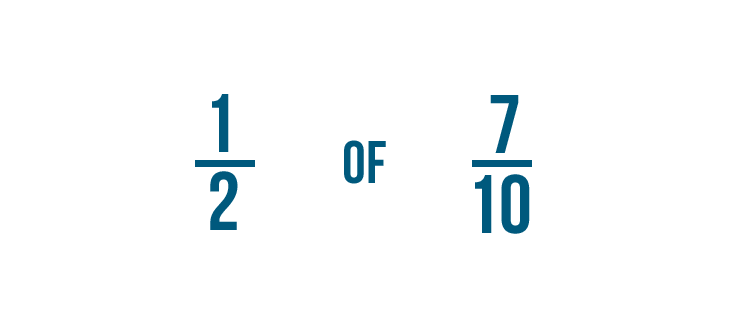
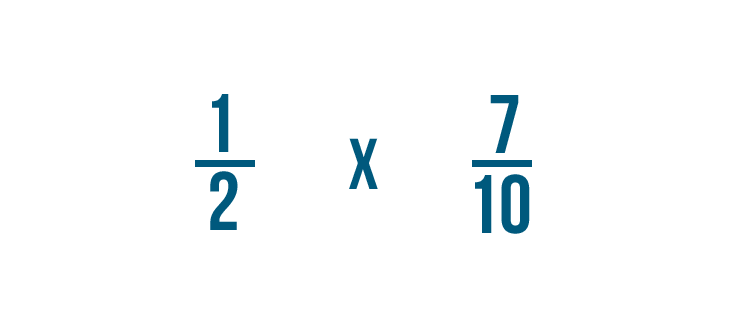
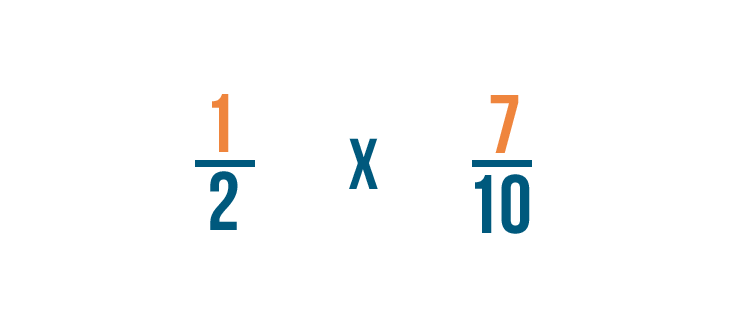
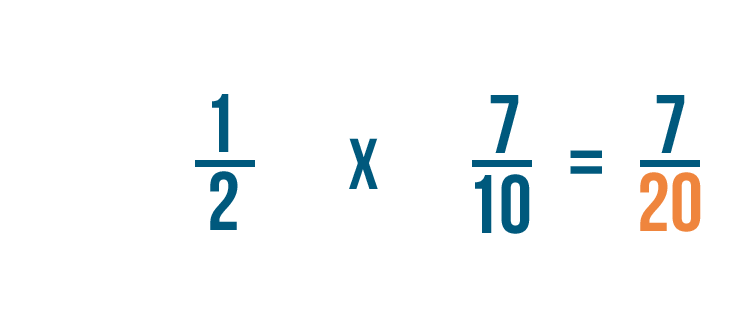
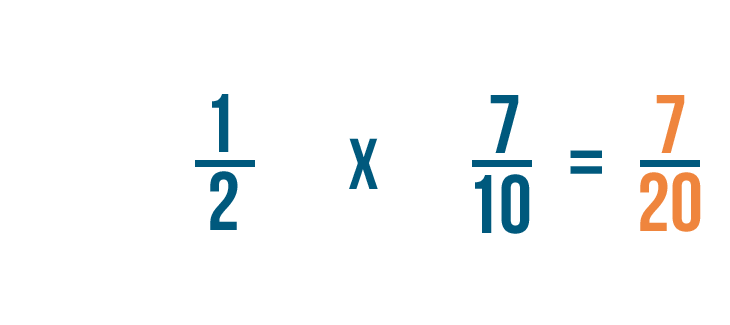
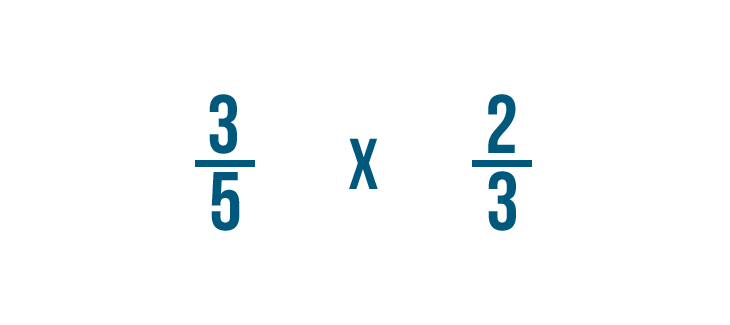
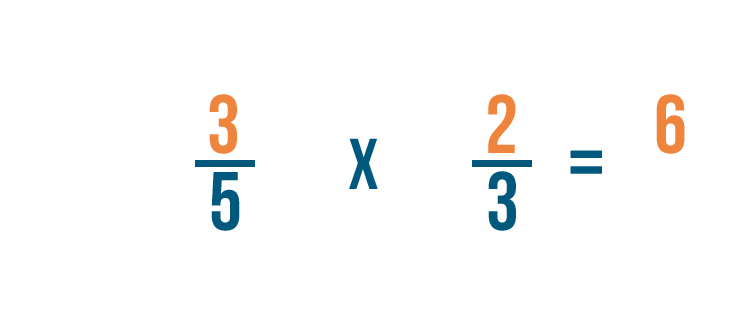
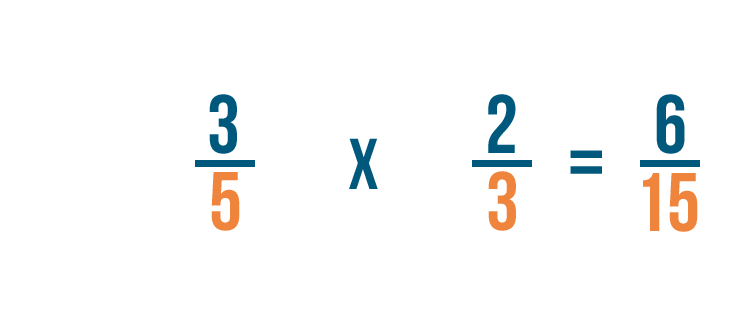
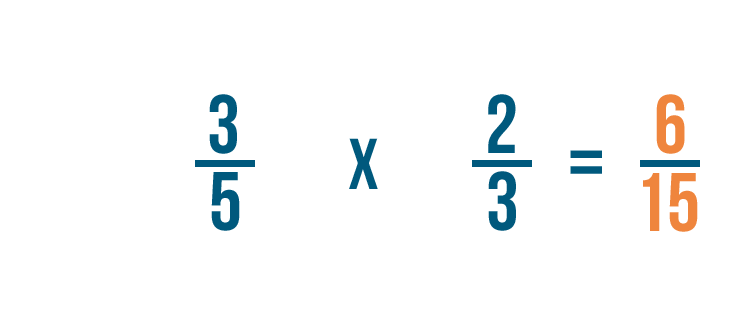
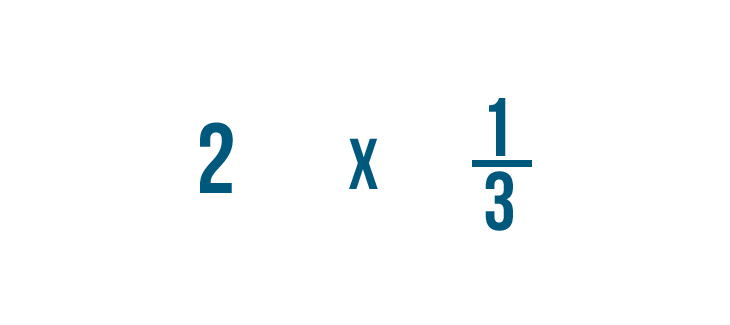
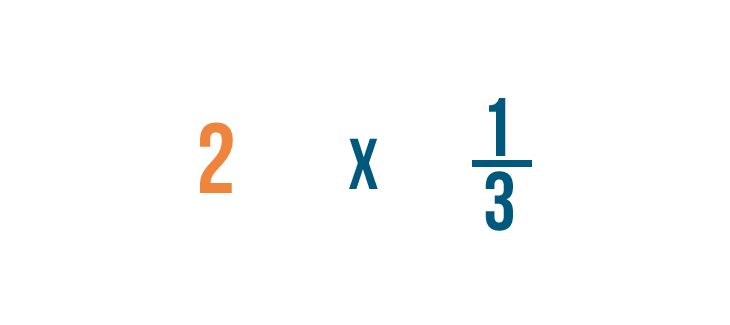
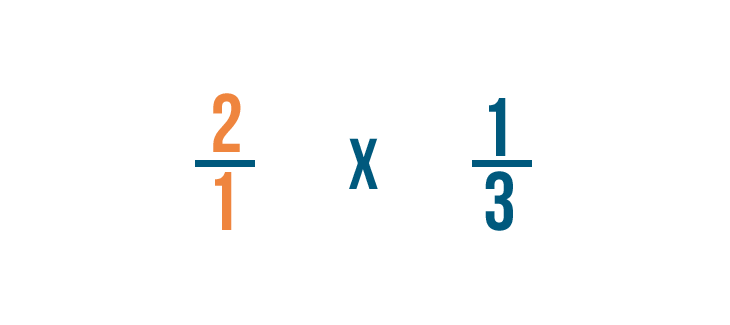
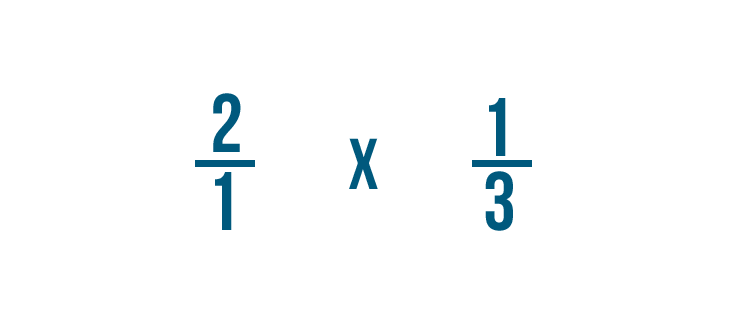
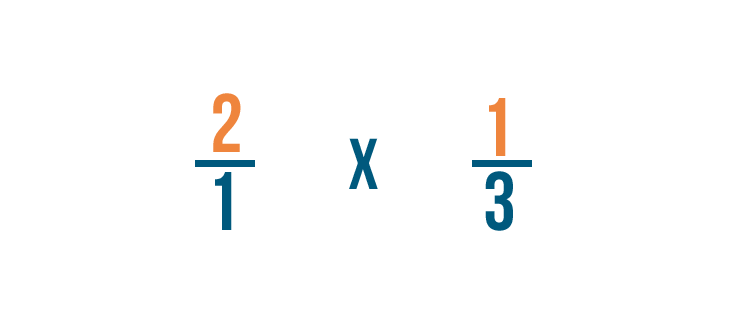
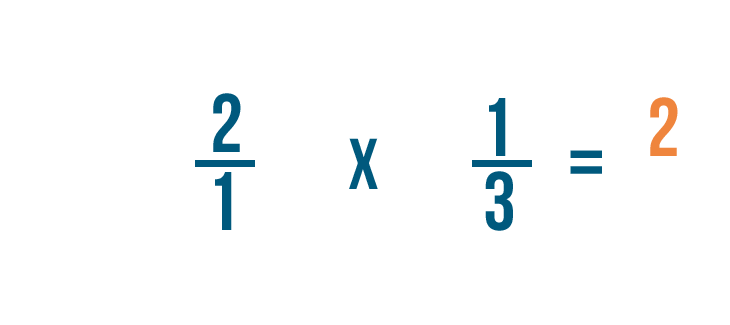
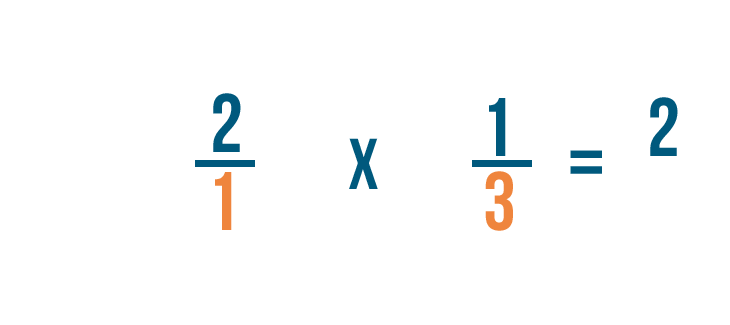
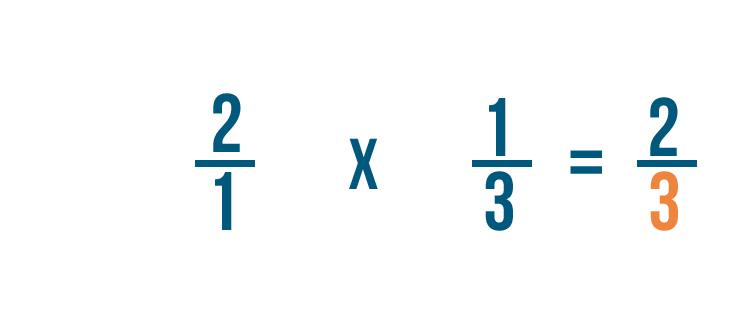
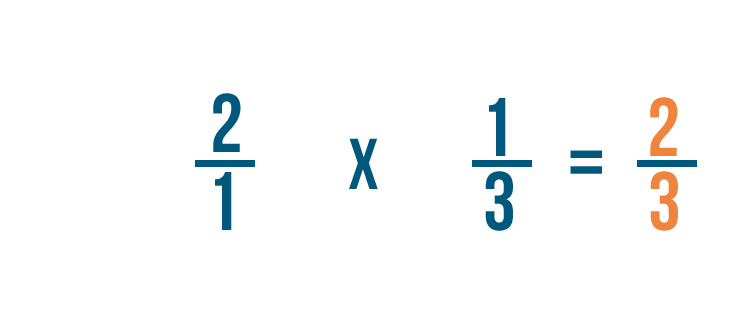
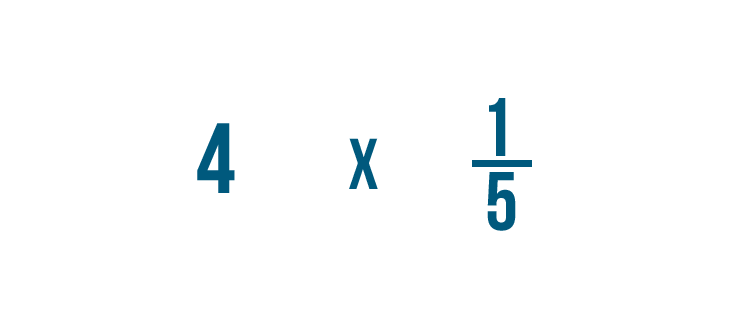
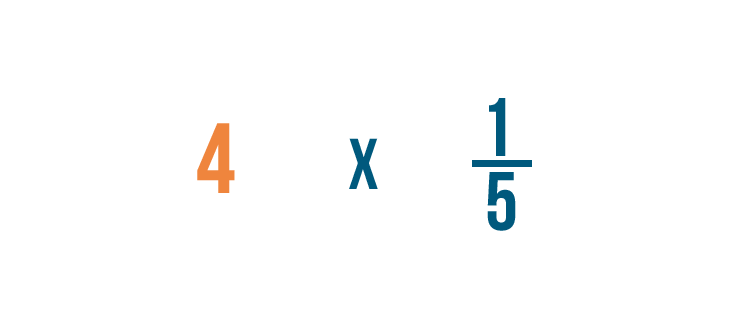
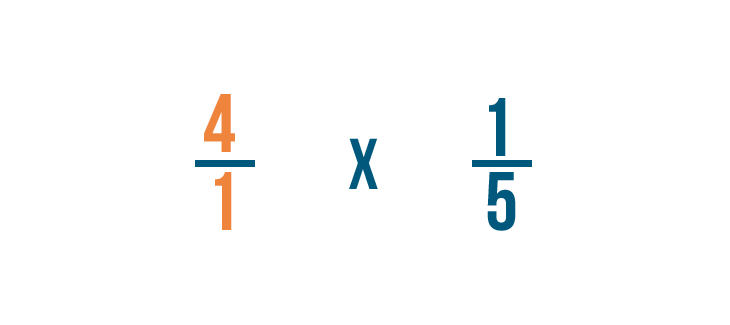
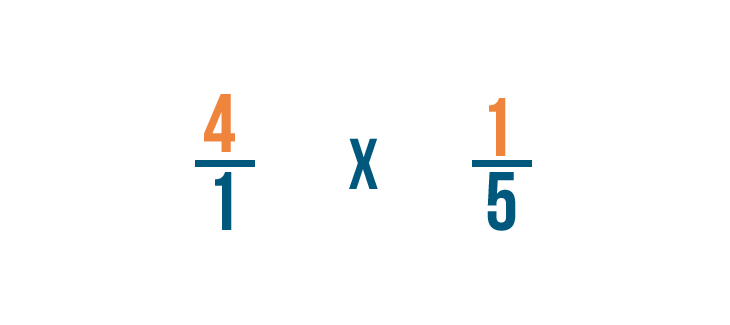
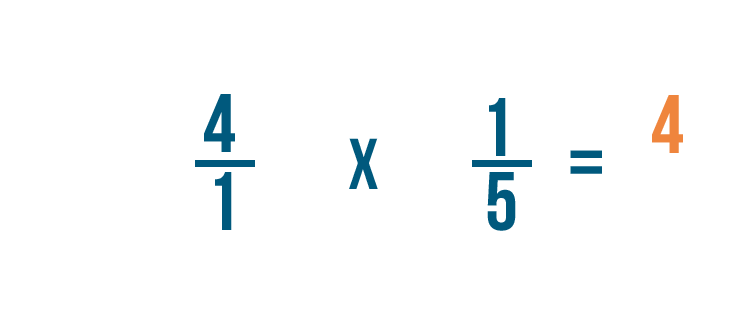
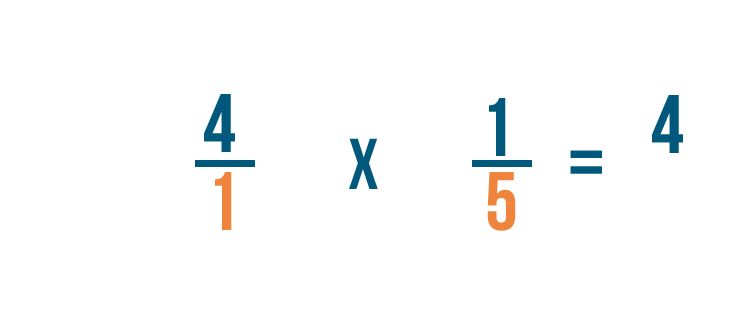
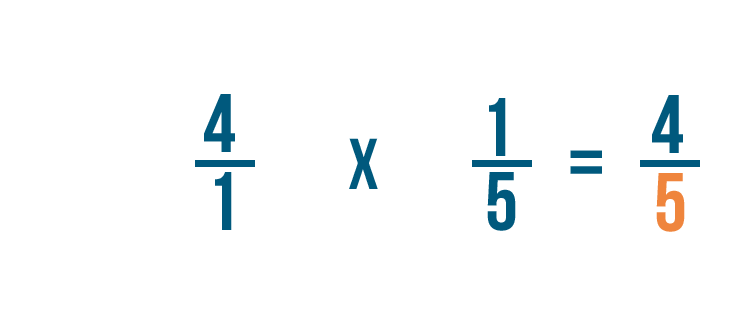
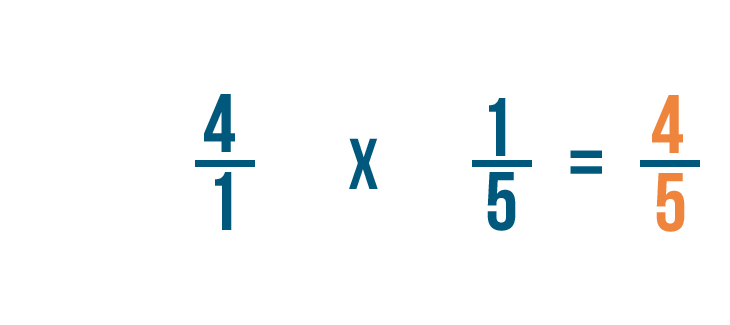
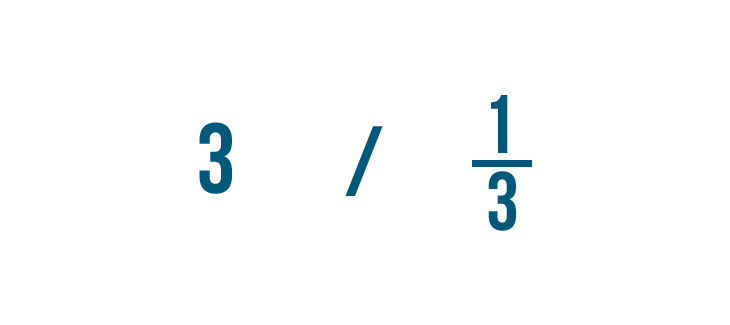
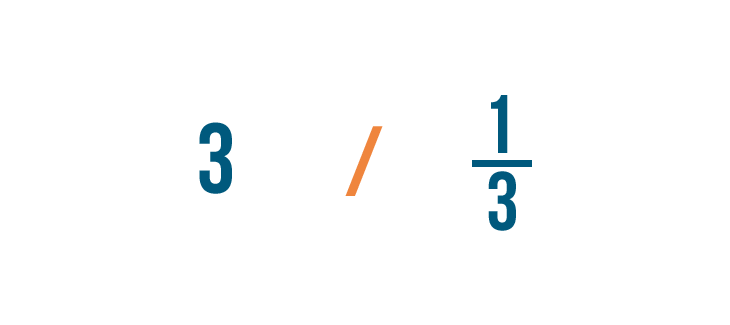
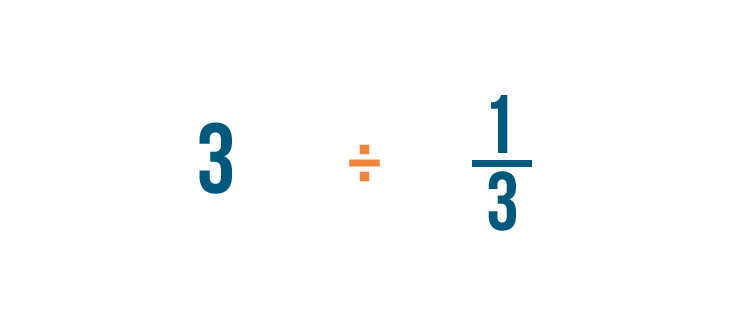
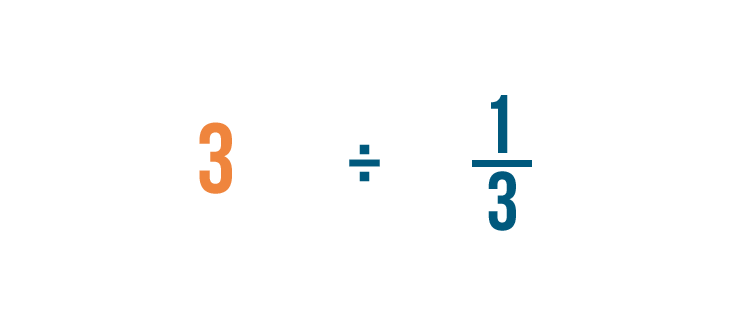
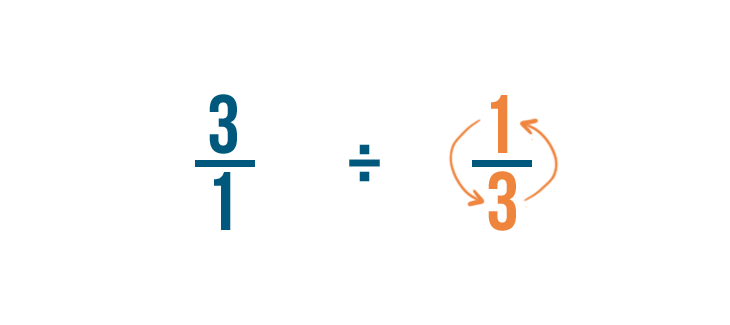
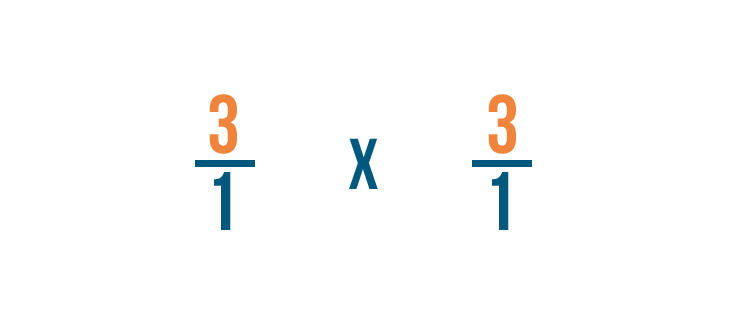
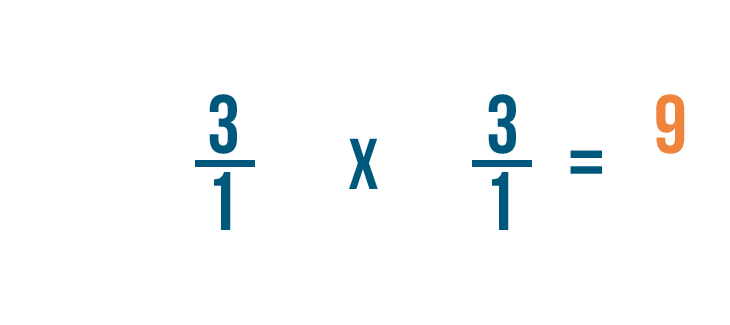
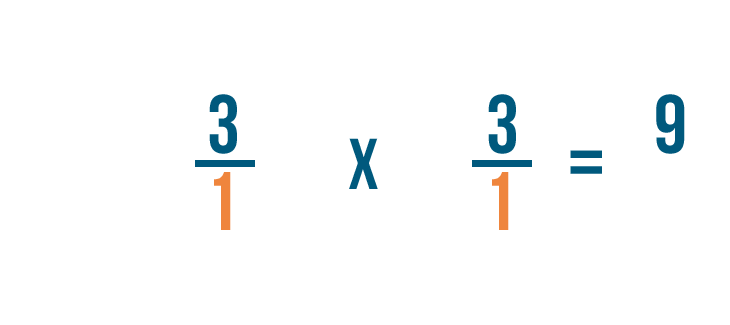
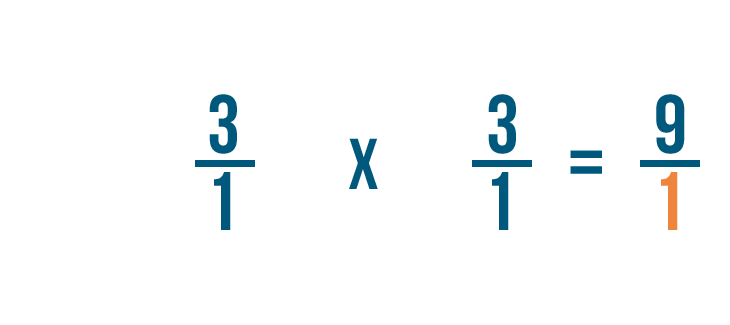
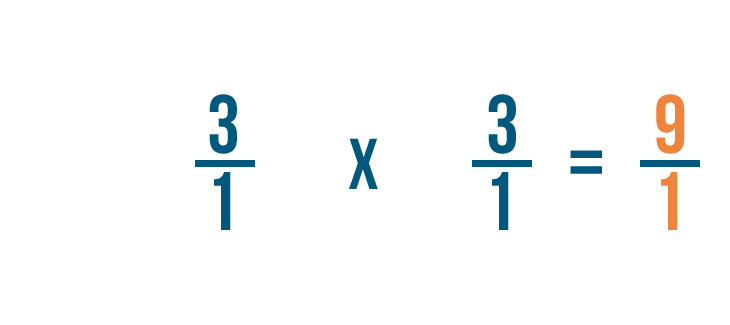
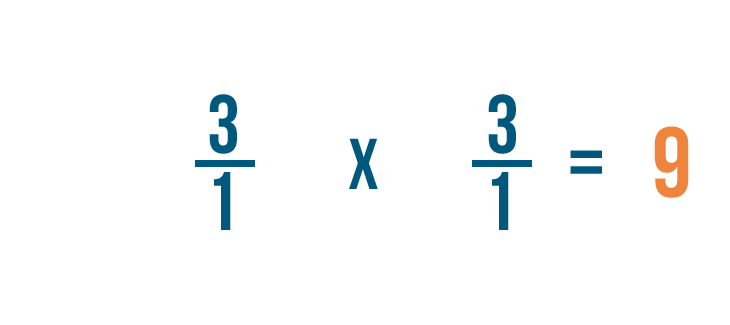
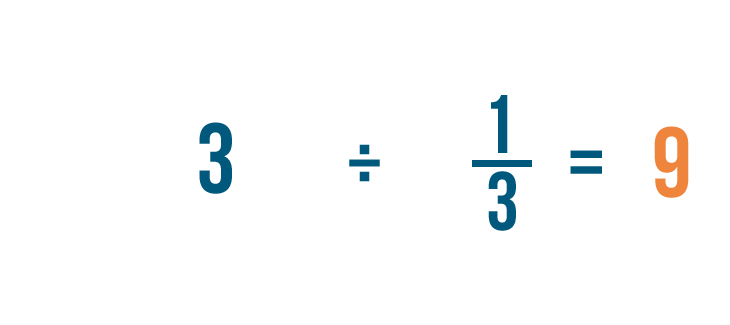
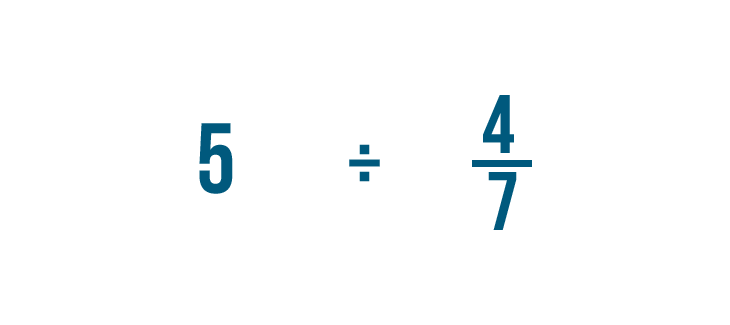
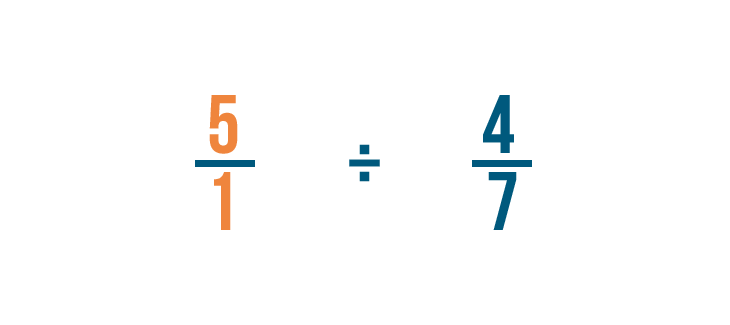
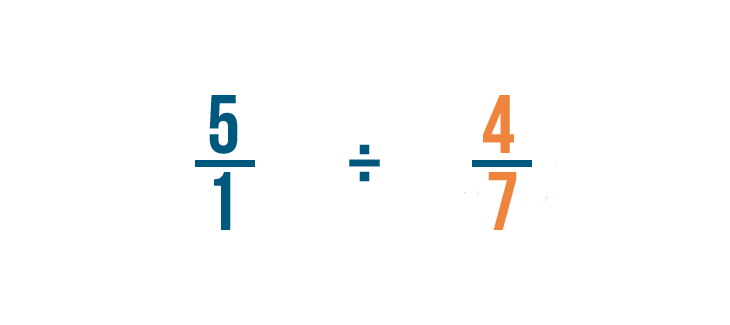
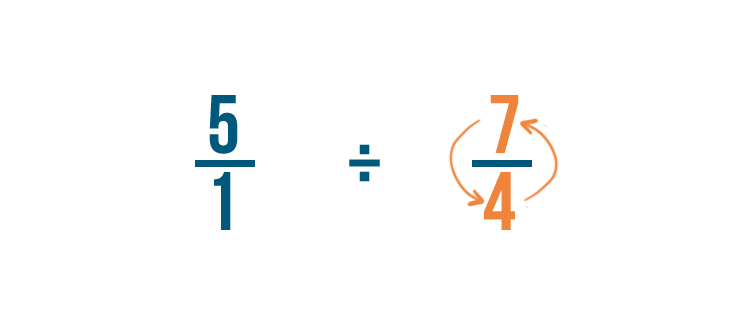
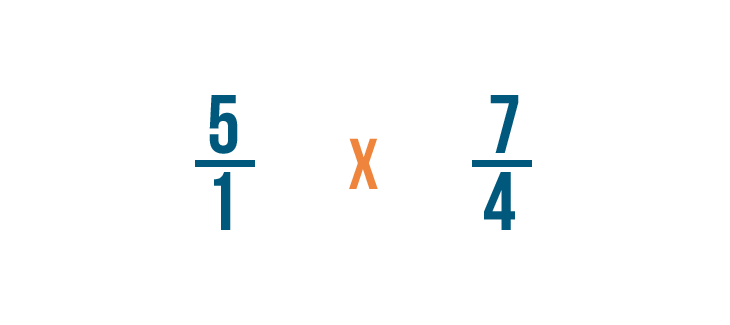
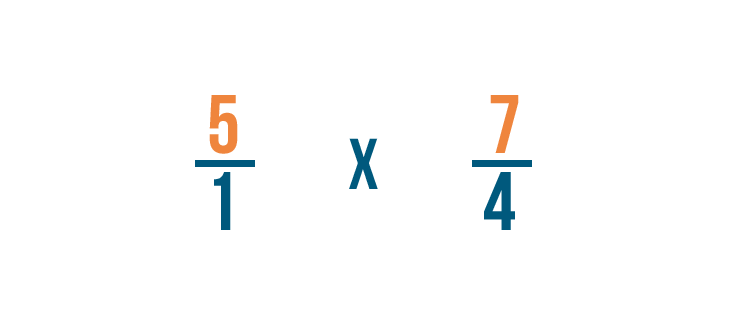
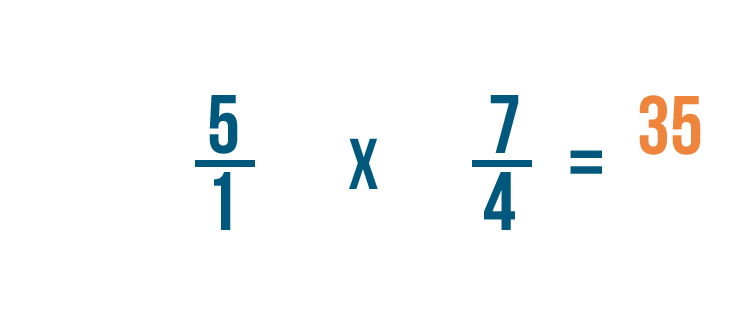
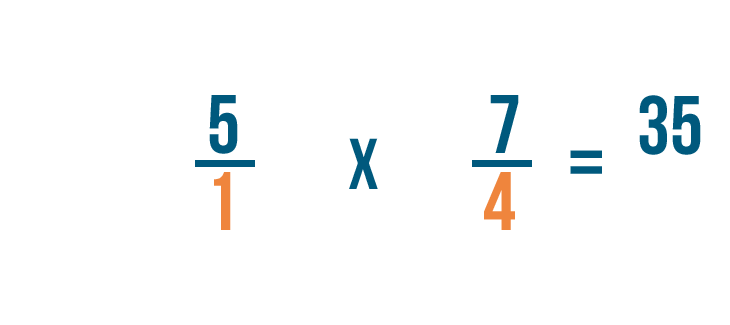
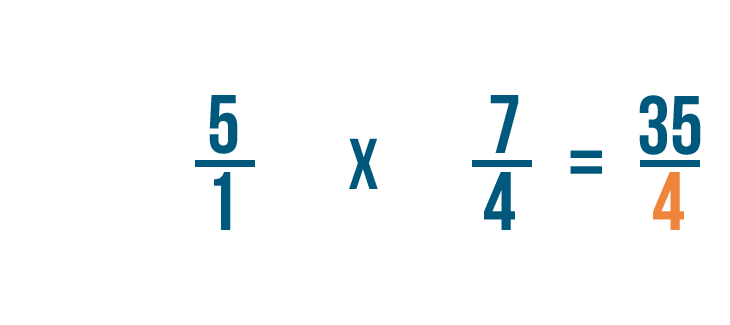
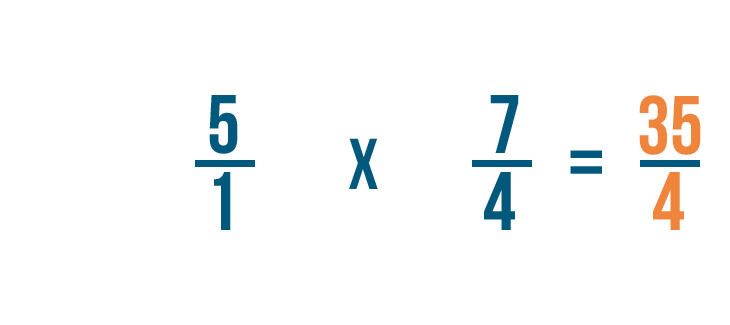
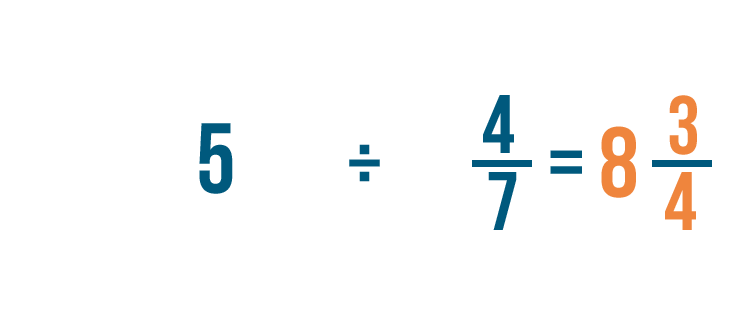
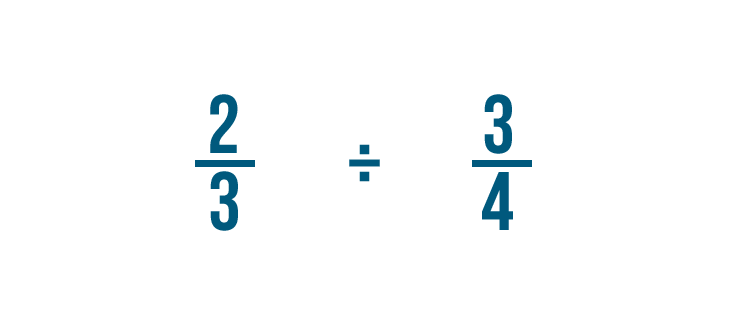
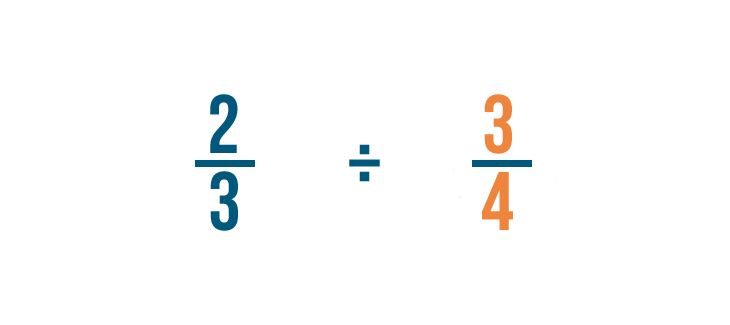
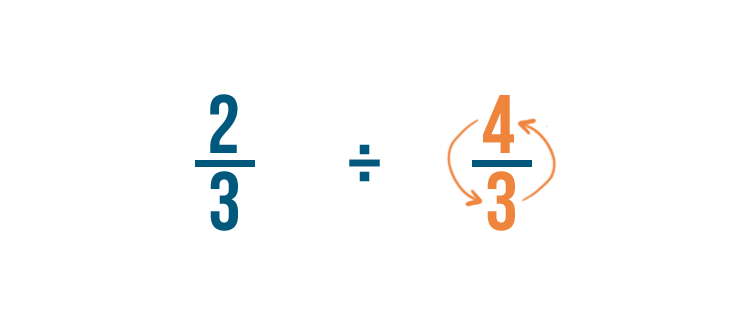
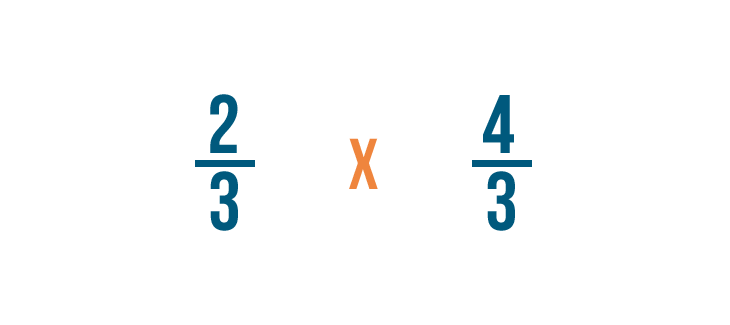
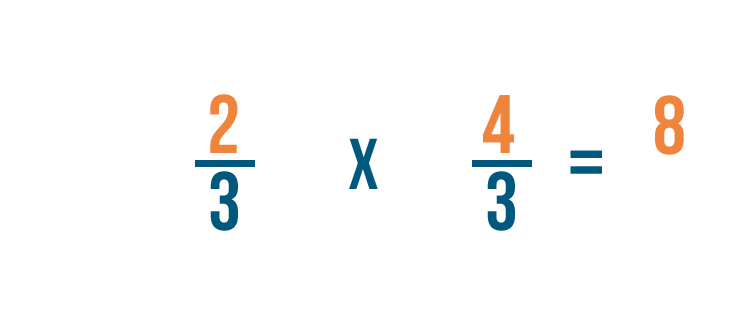
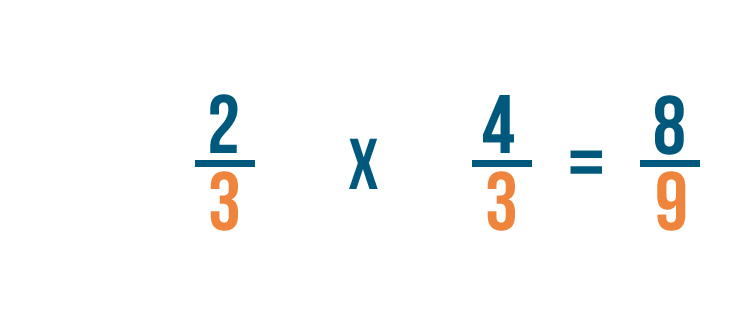
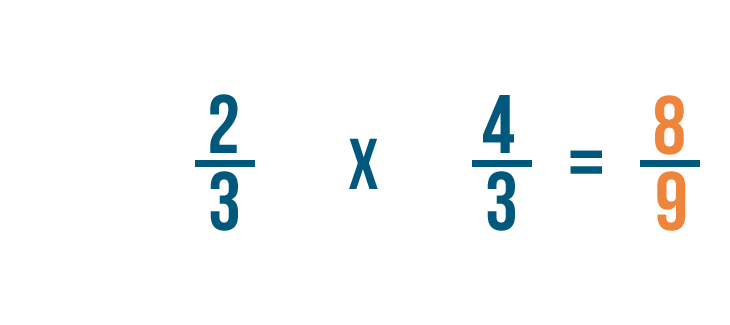
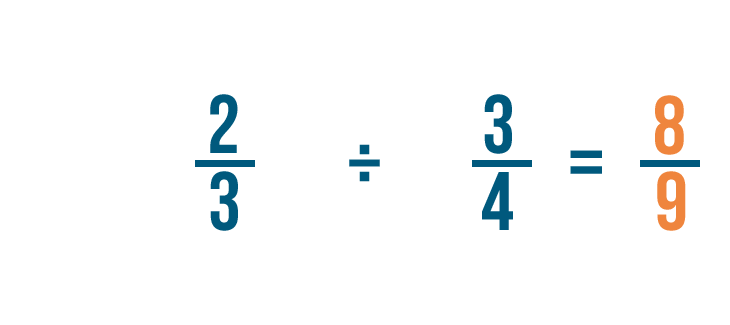
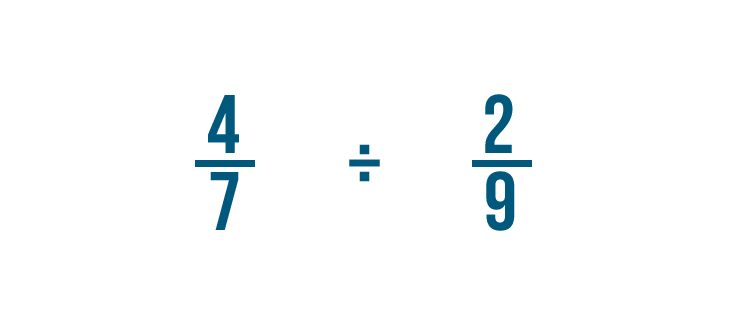
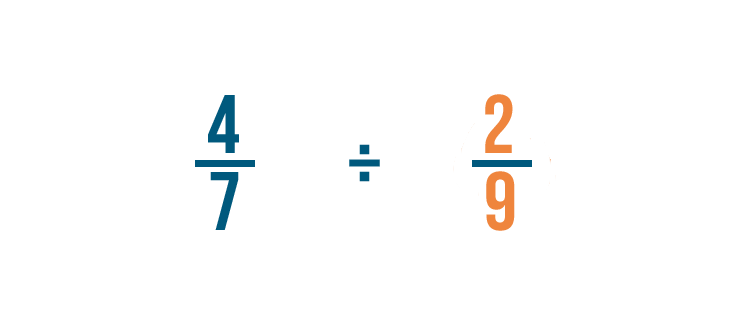
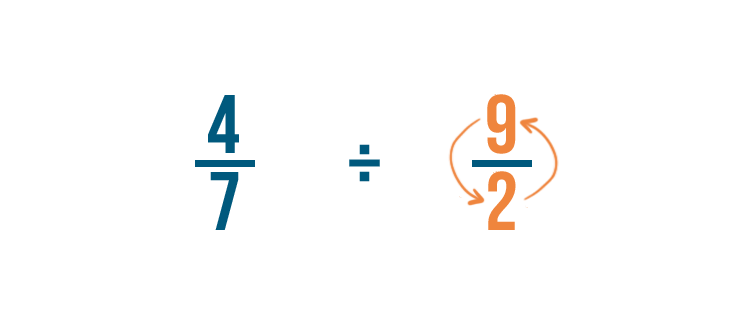
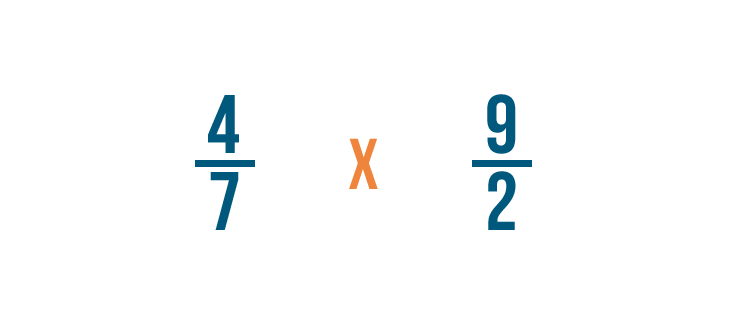
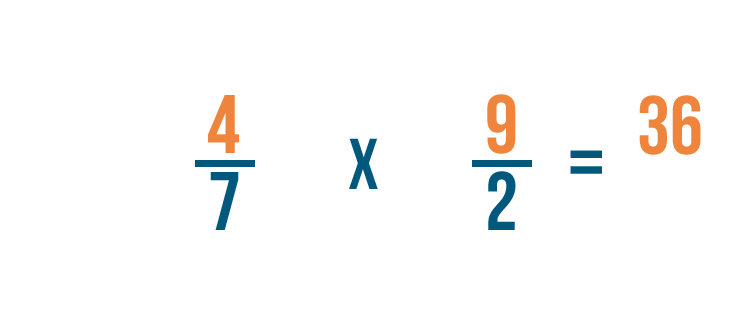
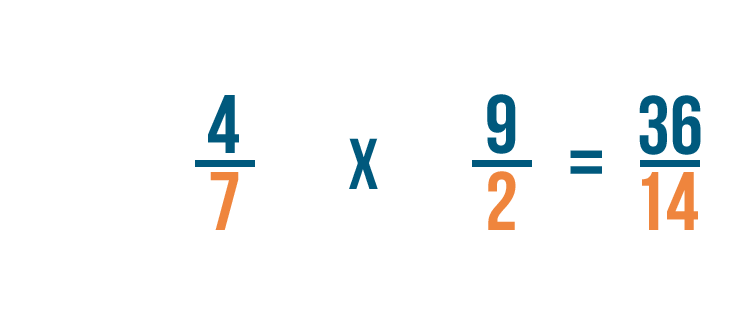
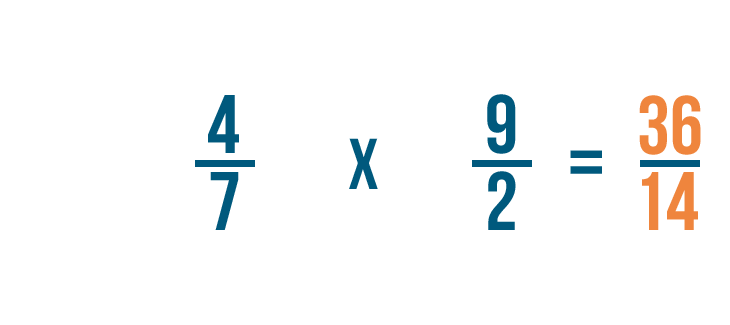
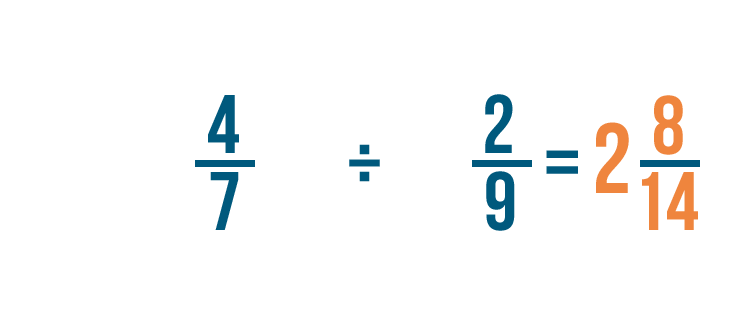

0 Response to "3 1 2 Times 3"
Post a Comment